Process Synchroniztion
Mutual Exclusion & Election Algorithms
October 31, 2018
Introduction
Process synchronization is the set of techniques that are used to coordinate execution among processes. For example, a process may need to run to a certain point, at which point it will stop and wait for another process to finish certain actions. A shared resource, such as a file or fields in a database, may require exclusive access and processes have to coordinate among themselves to ensure that access to the resource is fair and exclusive.
The modification of a resource may be implemented as an atomic operation. That is, there might be a single remote procedure call or web service that performs an operation on the resource. In this case, the server may be able to handle access to the resource on its own. In many cases, however, there might be concurrent requets on different servers that are competing for the same resource. There are also frequently situations where resource access is not inherently atomic and a client will need to request a lock on the resource and release it at a later time when all modifications are complete. Distributed transactions are an example of a framework that relies on this.
In centralized systems, it was common to enforce exclusive access to shared code. Mutual exclusion was accomplished through mechanisms such as test and set locks in hardware and semaphores, messages, and condition variables in software.
We will now visit the topic of mutual exclusion in distributed systems. We assume that there is group agreement on how a resource or critical section is identified (e.g., a name or number) and that this identifier is passed as a parameter with any requests. We also assume that processes can be uniquely identified throughout the system (e.g., using a combination of machine ID and process ID). The goal is to get a lock on a resource: permission to access the resource exclusively. When a process is finished using the resource, it releases the lock, allowing another process to get the lock and access the resource.
Any viable mutual exclusion algorithm must satisfy three properties:
- Safety
- This means the algorithm does indeed provide mutual exclusion. At any instant, only one process may hold the resource.
- Liveness
- The algorithm should make progress. Processes should not wait forever for messages that will never arrive.
- Fairness
- Each process should a fair chance to hold the resource. This means that a process that asks for a critical section should not wait forever to get it. No process should experience starvation. For example, two processes cannot transfer their lock on a resource back and forth to each other while a third process that wants the resource is denied from grabbing a lock.
There are three categories of mutual exclusion algorithms:
Centralized algorithms use a central coordinator. A process can access a resource because a central coordinator allowed it to do so.
Token-based algorithms move a token around. A process can access a resource if it is holding a token permitting it to do so.
Contention-based algorithms use a distributed algorithm that sorts out points of conflict (contention) where two or more processes may want access to the same resource.
Central server algorithm
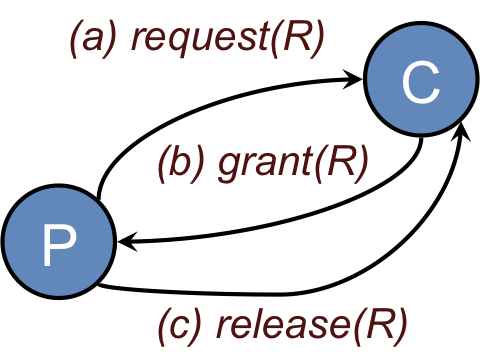
The central server algorithm simulates a single processor system. One process in the distributed system is elected as the coordinator (Figure 1). When a process wants to enter a resource, it sends a request message (Figure 1a) identifying the resource, if there are more than one, to the coordinator.
If nobody is currently in the section, the coordinator sends back a grant message (Figure 1b) and marks that process as using the resource. If, however, another process has previously claimed the resource, the server simply does not reply, so the requesting process is blocked. The coordinator keeps state on which process is currently granted the resource and a which processes are requesting the resource. The list of requestors is a first-come, first-served queue per resource. If some process has been granted access to the resource but has not released it, any incoming grant requests are queued on the coordinator. When a coordinator receives a release(R) message, it sends a grant message to the next process in the queue for resource R.
When a process is done with its resource, it sends a release message (Figure 1c) to the coordinator. The coordinator then can send a grant message to the next process in its queue of processes requesting a resource (if any).
This algorithm is easy to implement and verify. It is fair in that all requests are processed in order. Unfortunately, it suffers from having a single point of failure. Another issue is that a process cannot distinguish between being blocked (not receiving a grant because someone else is in the resource) and not getting a response because the coordinator is down. From the coordinator’s side, the coordinator does not know if a process using a resource has died, is in an infinite loop, or is simply taking a longer time to release a resource. Moreover, a centralized server can be a potential bottleneck in systems with a huge number of processes.
Token Ring algorithm
For this algorithm, we assume that there is a group of processes with no inherent ordering of processes, but that some ordering can be imposed on the group. For example, we can identify each process by its machine address and process ID to obtain an ordering. Using this imposed ordering, a logical ring is constructed in software. Each process is assigned a position in the ring and each process must know who is next to it in the ring (Figure 2). Here is how the algorithm works:
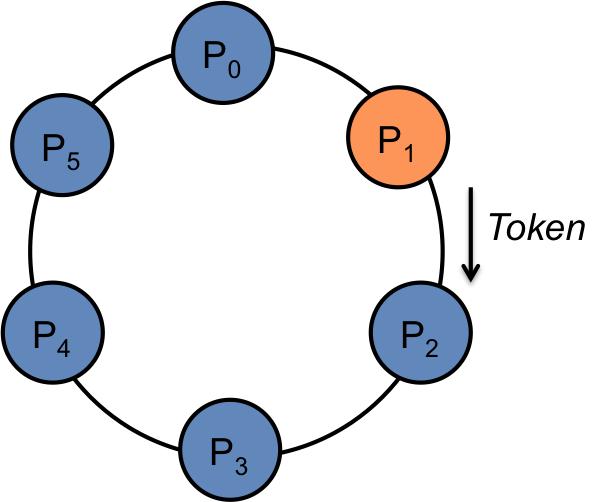
The ring is initialized by giving a token to process 0. The token circulates around the ring: process n passes it to process (n+1) mod ringsize.
When a process acquires the token, it checks to see if it is is waiting to use the resource. If so, it uses it and does its work. On exit, it passes the token to its neighboring process. In Figure 2, Process 1 had the token, completed its access to the resource, and is sending the token to its neighbor, process 2.
If a process is not interested in grabbing the lock on the resource, it simply passes the token along to its neighbor.
Only one process has the token, and hence the lock on the resource, at a time. Therefore, mutual exclusion is guaranteed. Order is also well-defined, so starvation cannot occur. The biggest drawback of this algorithm is that if a token is lost, it will have to be generated. Determining that a token is lost can be difficult.
Lamport’s mutual exclusion algorithm
Lamport’s mutual exclusion algorithm is the first of two contention-based mutual exclusion algorithms that we will examine. In this algorithm, every process in the group maintains a request queue. These is a list of processes that want to access a resource.
All messages are sent reliably and in FIFO order and each message is time stamped with unique Lamport timestamps. All items in the request queues are sorted by message timestamps.
The basic mechanism of this algorithm is that a process that wants to use the resource sends a timestamped request for the resource to all group members as well as to itself. Every recipient adds the received request to its request queue, which is sorted in timestamp order. Because all processes get all request messages, all timestamps are unique, and all queues are sorted, every process has the exact same items on its queue. If a process sees itself at the head of the queue, it knows that it can access the resource: no other process will be at the head of the queue. When it is done, it sends a release message to all group members and removes its ID from its local queue. Each group member, upon receiving a release message, removes that process ID from the request queue and checks to see whether it is at the head of the queue and can access the resource.
To summarize:
- To request a resource (ask for a lock)
- A process Pi sends a request(R, i, Ti) to all group members and places the same request on its own queue for resource R. When a process Pj receives a request message, it returns a timestamped acknowledgement (ack) and places the request on its request queue.
- To get the lock on the resource
- A process Pi must have received ack messages from everyone and its request must have the earliest timestamp in its request queue for resource R. If not, it waits.
- To release the resource lock
- A process Pi removes its own request from the head its queue for resource R and sends a release(R, i, Ti) message to all nodes. When each process receives the release message, it removes the entry for process i from its queue for resource R. The process then checks to see whether its own request is now the earliest one in (at the head of) its request queue. If it is, then the process now has the resource lock. If not, it has to wait.
Lamport’s algorithm is not a great one. We replaced the single point of failure of the centralized algorithm with an algorithm that has N points of failure. In addition, there is a lot of messaging traffic. Each request requires sending N–1 messages (one to each group member) and getting N–1 acknowledgements. Finally, when a resource lock is released, a process must send N–1 release messages.
Ricart & Agrawala distributed mutual exclusion algorithm
Ricart & Agrawala put forth a fully distributed mutual exclusion algorithm in 1981. It requires the following:
total ordering of all events in a system (e.g. Lamport’s timestamp algorithm with unique timestamps)
messages are reliable (the delivery of every message is acknowledged).
When a process wants to get a lock for a resource, it:
Composes a message containing { message identifier(machine ID, process ID), name of the resource, timestamp).
Sends a request message to all other processes in the group (using reliable messaging).
Wait until everyone in the group has given permission.
Access the resource; it now has the lock.
When a process receives a request message, it may be in one of three states:
- Case 1
- The receiver is not interested in the resource, send a reply (OK) to the sender.
- Case 2
- The receiver is in the resource. Do not reply but add the request to a local queue of requests.
- Case 3
- The receiver also wants the lock on the resource and has sent its request. In this case, the receiver compares the timestamp in the received message with the one in the message that it has sent out. The earliest timestamp wins. If the receiver is the loser, it sends a reply (OK) to sender. If the receiver has the earlier timestamp, then it is the winner and does not reply (and will get an OK from the other process). Instead, it adds the request to its queue and will send the OK only when it is done with its use of the resource.
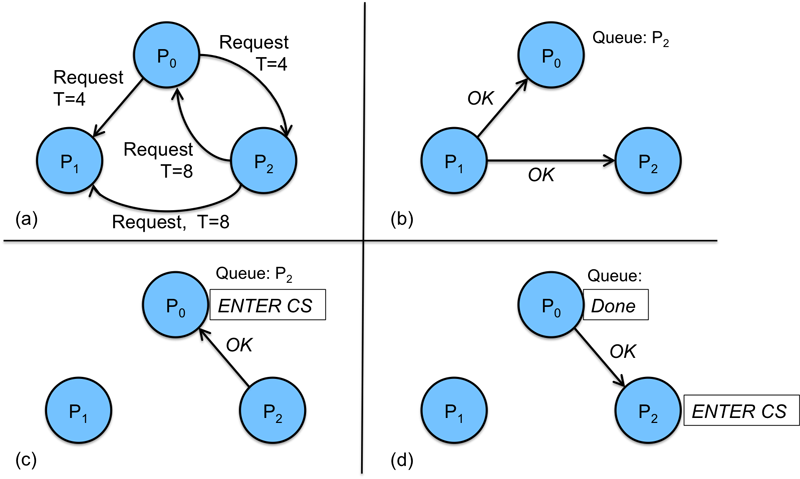
Figure 3 illustrates how the algorithm deals with contention. It shows a system of three processes. Processes 0 and 2 want the same resource at approximately the same time. Process 0 sends a request with a Lamport timestamp of 4. Process 2 sends a request with a timestamp of 8 (Figure 3a).
Process 1 is not interested in the resource, so it simply responds to both messages (Figure 3b).
When Process 0 receives the Request message from Process 2, it compares the timestamp on that message (8) with the timestamp in the message it sent (4). Since the timestamp in its message is earlier (it is immaterial whether P0 really did send the message earlier), it will not send a response to Process 2. Instead it adds Process 2 to a queue where it will hold all request messages until it is done with the resource. Meanwhile, when Process 2 compares timestamps, it finds that the timestamp on the message from Process 0 is less than the timestamp on its own process, so it is obligated to send a response to Process 0 and just wait to get all responses before it can get the lock and use the resource. Process 0 now gets responses from all processes and can use the resouce (Figure 3c).
When Process 0 is done with the resource, it sends a response to every process in its queue for that resource. In this case, only Process 2 is in the queue, so Process 2 gets a response. Now Process 2 has received responses from all processes and can use the resource (Figure 3d).
One problem with this algorithm is that a single point of failure has been replaced with n points of failure. A poor algorithm has been replaced with one that is essentially n times less reliable. All is not lost. We can patch this omission up by having the sender always send a reply to a message: either an OK or a NO. When the request or the reply is lost, the sender will time out and retry. Still, it is not a great algorithm and involves quite a bit of message traffic.
Both the Ricart & Agrawala and Lamport algorithms are contention-based algorithms. With Lamport’s algorithm, everyone immediately responds to a mutual exclusion request message whereas with the Ricart & Agrawala, a process that is using the resource will delay its response until it is done. This avoids the need to send release messages and reduces messaging traffic. The Ricart & Agrawala algorithm requires 2(N–1) messages while the Lamport algorithm requires 3(N–1) messages. The decision of whether a process has the lock on the resource is also different. The Lamport algorithm causes every process to have a replicated request queue and the decision of whether one has a lock is based on whether one is first (earliest) in that queue. With Ricart & Agrawala, the decision of whether one has a lock is based on whether acknowledgements have been received from everyone else in the group.
Election algorithms
We often need one process to act as a coordinator. It may not matter which process does this, but there should be group agreement on only one. An assumption in election algorithms is that all processes are exactly the same with no distinguishing characteristics. Each process can obtain a unique identifier (for example, a machine address and process ID) and each process knows of every other process but does not know which is up and which is down.
Bully algorithm
The bully algorithm selects the process with the largest identifier as the coordinator. It works as follows:
When a process p detects that the coordinator is not responding to requests, it initiates an election:
a. p sends an election message to all processes with higher numbers.
b. If nobody responds, then p wins and takes over.
c. If one of the processes answers, then p’s job is done.
If a process receives an election message from a lower-numbered process at any time, it:
a. sends an OK message back.
b. holds an election (unless its already holding one).
A process announces its victory by sending all processes a message telling them that it is the new coordinator.
If a process that has been down recovers, it holds an election.
Ring algorithm
The ring algorithm uses the same ring arrangement as in the token ring mutual exclusion algorithm, but does not employ a token this time. Processes are physically or logically ordered so that each knows its successor.
If any process detects failure, it constructs an election message with its process ID (e.g., its network address and local process ID) and sends it to its neighbor.
If the neighbor is down, the process skips over it and sends the message to the next process in the ring. This process is repeated until a running process is located.
At each step, the process adds its own process ID to the list in the message and sends the message to its living neighbor.
Eventually, the election message comes back to the process that started it. The process realizes this because it gets an election message with its own process ID at the head of the list. The list of processes in the message represents the list of all live processes in the system. The process then picks either the highest or lowest process ID in the list and sends out a message to the group informing them of the new coordinator. The method for picking the leader has to be consistent so that even if multiple election messages circulated, each process that started an election will come to the same decision on who the coordinator is.
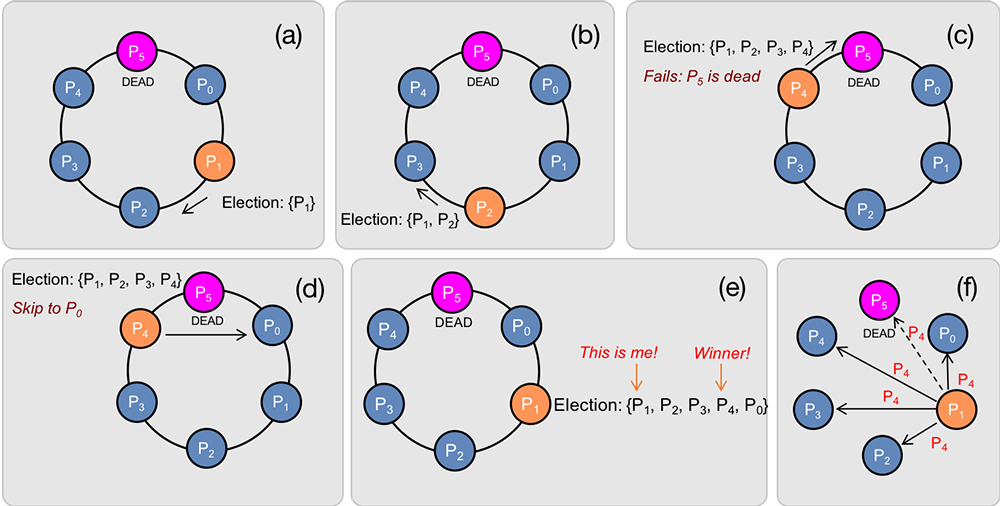
Figure 4 shows a ring of six processes (0–5). Process 1 detects that the coordinator, Process 5, is dead. It starts an election by sending an election message containing its process ID to its neighbor, Process 2 (Figure 4a).
Process 2 receives an election message and sends an election message to its neighbor with the ID of Process 2 suffixed to the list (Figure 4b).
The same sequence of events occurs with Process 3, which adds its ID to the list it received from Process 2 and sends an election message to process 4. Process 4 then tries to send an election message to Process 5 (Figure 4c).
Since process 5 is dead and the message is not delivered, Process 4 tries again to its neighbor once removed: Process 0 (Figure 4d).
Because Process 5 never received the election message, its ID does not appear in the list that Process 0 receives. Eventually, the message is received by Process 1, the originator of the election (Firgure 4e). Process 1 recognizes that it is the initiator of the election because its ID is the first in the list of processes.
It then picks a leader. In this implementation, it chooses the highest-numbered process ID in the list, which is that of process 4. It then informs the rest of the group of the new coordinator (Figure 4f).
Chang and Roberts Ring Algorithm
One inefficiency with the ring algorithm is that if multiple processes all discover a dead coordinator and start an election, multiple election messages will circulate concurrently. The Chang & Roberts Ring Algorithm optimizes the Ring algorithm to kill off election messages when it is safe to do so. That is, a process can kill (not forward) an election message if it knows that another message is circulating that will not be killed off by any other process.
With the Chang & Roberts algorithm, the coordinator selection is performed dynamically as the message circulates, so the election message contains only one process ID in it - the highest numbered one found so far. Think about the ring algorithm: if our goal is to pick the largest process ID to be the coordinator, there is no point in ever affixing smaller process IDs to the list in the message.
Every election message starts with the process ID of the process that started the message. If a process sends an election message, it identifies itself as a participant in the election regardless of whether it initiated the election or forwarded a received election message,
To pick the surviving process with the highest-numbered process ID, any process that detects the death of the current leader creates an election message containing its process ID and sends it to its neighbor, as was done in the ring algorithm. Upon receiving an election message, a process makes the following decision:
If the process ID of the message is greater than the process ID of the process, forward the message to the neighbor as in the ring algorithm. The current process is not a contender to become the coordinator since the election message tells us that a process ID with a higher number exists.
If the process ID of the message is less than the process ID of the process then replace the process ID of the message with the process ID of the process. Then forward the message to the neighbor as in the ring algorithm. This is the opposite of the previous decision. The current process has a higher process ID than any other process that encountered this election message, so it has a chance of becoming named coordinator.
If the process ID of the message is less than the process ID of the process and the process is already a participant, then discard the message. If the process is a participant, that means it already sent an election message to its neighbor with either itself or a higher-numbered process ID. Forwarding this message on would be redundant.
If the process ID of the message is the same as the process ID of the process, that means that the message has circulated completely around and no higher-numbered process encountered the message since it would have replaced the message’s ID with its process ID. The process therefore knows it is the coordinator and can inform the rest of the group.
Network partitioning
One thing to watch out for with election algorithms is network partitioning: the case where processes and machines do not die but a network of machines is segmented into two or more sub-networks that cannot communicate with each other. For example, a machine might become disconnected from the network or a connection between two switches or routers may break. In this case, the machines in each segment of the network will elect their own coordinator. This can lead to the launch of replicated processes, one for each network segment and a lack of any coordination between segments. Detecting whether a machine is dead or whether it is on a partitioned network requires using an alternate communication mechanism, such as a redundant network or some shared resource to which all group members can read and write.
References (partial)
Distributed Systems: Concepts and Design, G. Coulouris, J. Dollimore, T. Kindberg, (c) 1996 Addison Wesley Longman, Ltd., pp. 300–309 (section 10.4)
Distributed Operating Systems, Andrew Tanenbaum, (c) 1995 Prentice Hall.
This is an updated version of a document originally created on November 4, 2012.