Introduction

Before we jump into Bitcoin, we will introduce two storage structures that Bitcoin uses: blockchains and Merkle trees. Both are built using hash pointers.

Hash Pointers

A cryptographic hash serves as a checksum for a message. If a message has been modified, it will yield a different hash. By associating a hash with a message, we have a basis for managing the integrity of that message: being able to detect if the message gets changed.

One way of associating a hash with a message is with the use of hash pointers. Pointers are used in data structures to allow one data element to refer to another. In processes, a pointer is a memory location. It could also be an object reference like a file name. In distributed systems, a pointer may be the name or IP address of a computer along with an object identifier. A hash pointer is a tuple that contains a traditional pointer (reference) along with the hash of the data element that is being pointed to. It allows us to validate that the information being pointed to has not been modified.

Tamper-resistant linked lists: blockchains

The same structures that use pointers can be adapted to use hash pointers to create tamper-evident structures. For example, a linked list can be constructed with each element containing a hash pointer to the next element instead of a pointer.

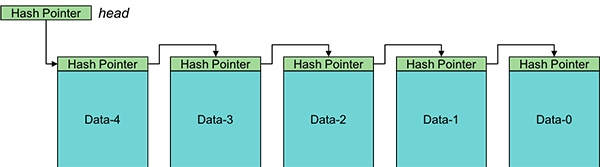
Adding a new block is easy. You allocate the block, copy the head hash pointer into it (the next pointer), and update the head hash pointer to point to the new block and contain a hash of that block.

If an adversary modifies, say, data block 1, we can detect that. The hash pointer in Data-2 will point to Data-1, but the hash of Data-1 will no longer match the hash in the pointer. For a successful attack, the adversary will also need to modify the hash value in the hash pointer in block 2. That will make the hash pointer in block 3 invalid, so that will need to be changed.

The adversary will need to change all the hash pointers leading up to the head of the list. If we can protect the head of the list (e.g., in a variable or some trusted storage) so that the adversary cannot modify it, then we will always be able to detect tampering. A linked list using hash pointers is called a blockchain.

Merkle Trees

Another useful structure using hash pointers in place of conventional pointers is a binary tree, called a Merkle tree when implemented with hash pointers.

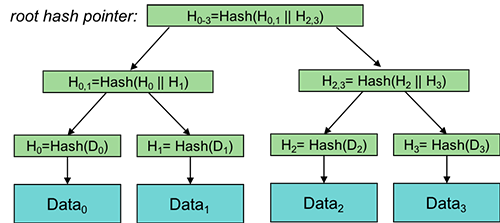
Leaf nodes of a Merkle tree contain conventional hash pointers: pointers to the data blocks and the hashes of those data blocks. Non-leaf child nodes contain left and right pointers along with the hash of the two hashes they point to (for example, a hash of the concatenation of the two hashes).

This process continues upward, creating a root hash (Merkle root) that represents the entire dataset.

Any change in a data block changes its hash, which alters all parent hashes up to the root, allowing easy detection of tampering. Only the root hash (the Merkle Root) has to be obtained in a trustworthy manner because any modifications could be detected by traversing from the root hash.

Merkle trees are efficient for verifying data integrity because only a subset of the hashes (not the entire tree) needs to be checked to validate individual data blocks, making them ideal for decentralized systems and secure data verification in limited-bandwidth environments.

Similarly. Merkle trees make it efficient to check whether data belongs to a larger data set. Merkle trees are used for this purpose in Bittorrent and Git.

Applications of blockchains and Merkle trees

Merkle trees are useful in services that require secure and efficient verification of content in a large body of data. By organizing a binary tree structure, where each leaf node represents a hash of a data block and each non-leaf node is a hash of its child nodes, Merkle trees allow for the verification of specific data content by checking only a small portion of the tree. This is useful in checking the integrity of a specific transaction in a block of transactions, a specific file in a set of files, or the integrity of a piece of a file even if the entire content has not been downloaded.

Hash pointers are all about helping assess the integrity of data. Structures such as blockchains (hash-pointer-based linked lists) and Merkle trees were designed with peer-to-peer systems in mind where data can come from untrusted peers. You just need to get the root hash from a trusted place.

The top-level pointer (the root pointer in the case of a tree; the head pointer in the case of linked lists) represents the integrity of the entire set of data. If any data block changes, that top-level pointer will allow the user to detect that there has been a change. Therefore, this value must be stored securely and obtained via a trustworthy mechanism.

A Merkle tree allows you to check the integrity of replicated data on a branch-by-branch basis in an efficient manner. Merkle trees are designed for environments where data is replicated among multiple systems and you want each system to be able to validate the integrity of the entire file. This helps in two cases:

1. You can validate downloaded data without having to wait for the entire set of data to be downloaded as long as you have the Merkle tree (which will generally be small compared with the size of the underlying data, since it’s just a tree of hashes).

2. You can efficiently compare your data with that stored on another system.

Suppose you have a file and want to check whether any blocks in your version are corrupted with respect to a version on another server. Both you and another system assembled your own structure of hash pointers.

With a linked list of hash pointers, you’d start at the head of the list and compare hashes. If the hashes match, you are confident that your files match. If you have a mismatch, you need to compare the next hash. If it matches what you have then you know that first block has been modified. If it doesn’t then you need to get the hash after that. Ultimately, you may need to traverse the entire list linearly.

With Merkle trees, it becomes easier to find the block (or blocks) that have changed. If the root hash matches, you know that your entire data set matches. If not, you request the left & right hashes and compare those with your tree. If one doesn’t match then you can compare the hashes under that subtree, iterating down the tree until you find the mismatched data block. You do not need to iterate through the entire list of blocks. This is attractive for replicated data sets where we may have millions of data blocks, for example, and sending a hash list is not efficient. It essentially enables a tree search to find the block that is inconsistent.

For example, to see if the block Data₂ belongs in the data set, we take its hash (H₂). We have the entire Merkle Tree but only trust the root hash to be secure, so we then generate the hash one level up: H_2,3=Hash(H₂||H₃). Then we generate the top-level hash H_0–3=Hash(H_0,1||H_2,3). If the top-level hash matches the one we obtained securely, then we trust that the lower-level hashes we used and those we computed are indeed legitimate.

Merkle trees are particularly useful for obtaining data from multiple untrusted sources. For example, they are used by Bitcoin and Ethereum servers to migrate copies of the transaction log (the blockchain). They are also used for data replication by a variety of NoSQL databases and by the Git version control system. Given a valid root (top-most) hash pointer, the remaining hash tree can be received from any untrusted source. The receiver can simply validate by checking hashes up to the root. Now that the receiver has the entire tree, any data blocks can be received from untrusted sources as well. Each block can be validated by comparing its hash with the hash at the leaf node of the Merkle tree.

Bitcoin

Bitcoin was introduced anonymously in 2009 by a person or group under the pseudonym Satoshi Nakamoto and is considered to be the first blockchain-based cryptocurrency. Bitcoin was designed as an open, distributed, public system. There is no authoritative entity and anyone can participate in operating the servers.

Traditional payment systems rely on banks to serve as a trusted third party. If Alice pays $500 to Charles, the bank, acting as a trusted third party, deducts $500 from Alice’s account and adds $500 to Charles' account. Beyond auditing, there is no need to maintain a log of all transactions; we simply care about tracking account sums. With a centralized system, all trust resides in this trusted third party. The system fails if the bank disappears, the banker makes a mistake, or if the banker is corrupt.

With Bitcoin, the goal was to create a completely decentralized, distributed system that allows people to manage transactions while preventing opportunities for fraud. People have attempted this previously, using private keys to create digitally signed “coins” but the problem has been to figure out how to use them in a way that doesn’t allow double spending: to keep someone from spending the same coins for two different places. Solutions to this required a third party. Bitcoin solved the problem without the need for a trusted party.

The ledger and the Bitcoin network

Bitcoin maintains a complete list of every single transaction since its creation in January 2009. This list of transactions is called the ledger and is stored in a structure called a blockchain. Complete copies of the ledger are replicated at Bitcoin nodes around the world. There is no concept of a master node or master copies of the ledger. All of these systems run the same software. New systems get the names of some well-known nodes when they download the software and DNS query on these nodes returns their IP addresses. After connecting to one or more nodes, a Bitcoin node will ask each for a list of known Bitcoin nodes. This creates a peer discovery process that allows a node to get a complete list of other nodes in the network.

User identities and addresses

We know how to create unforgeable messages: just sign them. If Alice wants to transfer $500 to Charles, she can create a transaction record that describes this transfer and sign it with her private key (e.g., use a digital signature algorithm or create a hash of the transaction and encrypt it with her private key). Bitcoin uses public-private key pairs and digital signatures to sign transactions¹.

Bitcoin transactions — the movement of bitcoins from one account to another — are associated with public keys and not users. Users are anonymous. Your identity is your public key and you can use this identity by proving they have the corresponding private key.

There is never any association of your public key with your name or anything else that identifies you. In fact, nothing stops you from creating multiple key pairs and having many identities. The system does not care, or know, what your physical identity is or how many addresses you assigned to yourself. All that matters is that only you have the corresponding private keys to the public keys identified in your transactions so you are the only one who could have created valid signatures for your transactions.

If you can create transactions on behalf of a specific public key, it means that you own the corresponding private key. If you lose that private key, then you can no longer create transactions and hence cannot access your Bitcoin funds. There is nobody to call to recover a lost key since you are solely responsible for storing it!

Bitcoin identifies recipients of payments by their Bitcoin address. Your Bitcoin address is essentially a hash of your public key (and you will have several addresses if you have several keys; one for each key). The details of creating an address are a bit cumbersome:

1. Generate an ECDSA (Elliptic Curve Digital Signature Algorithm) public, private key pair. This serves as your identity and signing key.

2. Create a SHA-256 hash of the public key

3. Perform a RIPEMD-160 hash on that

4. Add a version byte in front of the result

5. Perform a SHA-256 hash on the result … and another SHA-256 hash on that result

6. The four bytes of the result are treated as the address checksum. Add these four bytes to the end of the RIPEMD-160 hash from [4]

7. Convert the bytes to a base-58 string using Base58Check encoding to create a 20-byte printable string. Base58Check encoding adds a checksum to be able to validate that the value is not mistyped. This string is your bitcoin address. It’s more compact than the corresponding public key.

When all is said and done, the address is simply a hash of your public key. Since a hash is a one-way function, someone can create (or verify) your address if they are presented with your public key. However, they cannot derive your public key if they have your address.

The original Bitcoin paper used a user’s public key as their identity. You would create a transaction that transfers some amount of bitcoin to someone whom you identify with their public key. Since then, there have been several versions of techniques for creating addresses and Bitcoin still also supports using a public key directly as an address.

Even though someone cannot derive a public key from an address, the Bitcoin ledger is publicly viewable, so someone only needs to find a transaction that contains a user’s public key within it. The usefulness of an address is twofold. First, it is shorter than a public key: 24 bytes instead of 32 bytes and can be represented as a 20-byte printable string. Secondly, it contains a checksum within it to enable the detection of typing errors; it is possible to validate if an address is incorrect.

• Alice’s transaction will identify where the money comes from (inputs). Each input contains a reference to a past transaction. The transaction contains Alice’s public key, and her signature.

• A node can validate the signature by using Alice’s public key, which is placed in the transaction. This proves that someone who owns the private key (Alice) that corresponds to that public key created the transaction.

• That transaction input references an older transaction where Alice’s address is identified as the output of the bitcoin. Given the address, we cannot derive the public key.

• A bitcoin node can hash Alice’s public key (from the input) to create the address and check that it is the same as in the output of the referenced old transaction. That way, it validates that the older transaction indeed gave money to Alice.

Bitcoin uses addresses only as destinations; an address can only receive funds. If Bob wants to send bitcoin to Alice, he will identify Alice as the output – the target of the money – by using her address. At some point in the future, Alice can use that money by creating a transaction whose source (input) refers to the transaction where she received the bitcoin. Any bitcoin node can validate this transaction:

User transactions (moving coins)

A transaction contains inputs and outputs. Inputs identify where the bitcoin comes from and outputs identify where to whom it is being transferred. If Alice wants to send bitcoin to Bob, she creates a message that is a bitcoin transaction and sends it to one or more bitcoin nodes. When a node receives a message, it will forward the transaction to its peers (other nodes it knows about). Typically, within approximately five seconds, every bitcoin node on the network will have a copy of the transaction and can process it.

The bitcoin network is not a database. It is build around a ledger, the list of all transactions. There are no user accounts that can be queried. In her transaction, Alice needs to provide one or more links to previous transactions that will add up to at least the required amount of bitcoin that she’s sending. These links to earlier transactions are called inputs. Each input is an ID of an earlier transaction. Inputs are outputs of previous transactions.

Alice’s account balance is the sum of all transactions that sent her money (she is an output) minus the all the money she spent (the money she used as inputs). It’s the sum of unspent transaction outputs (UTXO).

When a bitcoin node receives a transaction, it performs several checks:

1. The signature of each input is validated by checking it against the public key in the transaction. This ensures that it was created by someone who has the private key that corresponds to the public key.

2. It hashes the public key in the transaction to create the address, which will be matched against the output addresses in the inputs listed in the transaction.

3. The transactions listed in the inputs are validated to make sure that those transactions have not been used by any other transaction. This ensures there will be no double spending.

4. Finally, it makes sure that there is a sufficient quantity of bitcoin output by those input transactions.

A bitcoin transaction contains:

One or more inputs:

Each input identifies transactions where coins come from. These are references to past transactions. Bitcoin allows each input to contain a signature and a public key that corresponds to the private key that was used to create that signature. This is because a user may have multiple identities (keys) and may reference past transactions that were directed to different addresses that belong to the user.

Output:

Destination address & amount – who the money goes to. This is simply the recipient’s bitcoin address.

Change:

The transaction owner’s address & bitcoin amount. Every input must be completely spent. Any excess is generated as another output to the owner of the transaction.

Transaction fee (anywhere from 10¢ to a $10+ per transaction). There is a limited amount of space (about 1 MB) in a block. A transaction is about 250 bytes. To get your transaction processed quickly, you need to outbid others.

Blocks and the blockchain

Transactions are sent to all the participating servers. Each system keeps a complete copy of the entire ledger, which records all transactions from the very first one. Currently the bitcoin ledger is over 600 GB and contains over 1 billion transactions.

Transactions are grouped into a block. A block is just a partial list of transactions. When a server is ready to do so, it can add the block to the ledger, forming a linked list of blocks that comprise the blockchain. In Bitcoin, a block contains ten minutes worth of transactions, all of which are considered to be concurrent.

Approximately every ten minutes, a new block of transactions is added to the blockchain. A block is approximately a megabyte and holds, on average, a bit over 2,000 transactions. To make it easy to locate a specific transaction within a block, the blocks are stored in a Merkle tree. This is a binary tree of hash pointers and makes it easy not just to locate a desired transaction but to validate that it has not been tampered by validating the chain of hashes along the path.

Securing the Block

A critically important part of the Bitcoin blockchain is to ensure that blocks in the blockchain have not been modified. We explored the basic concept of a blockchain earlier. Each block contains a hash pointer to the previous block in the chain. A hash pointer not only points to the previous block but also contains a SHA-256² hash of that block. This creates a tamper-proof structure. If the contents of any block are modified (accidentally or maliciously), the hash pointer that points to that block will no longer be valid (the hashes won’t match).

To make a change to a block, an attacker will need to modify all the hash pointers from the most recent block back to the block that was changed. One way to prevent such a modification could have been to use signed hash pointers to ensure an attacker cannot change their values. However, that would require someone to be in charge of signing these pointers and there is no central authority in Bitcoin; anyone can participate in building the blockchain. We need a different way to protect blocks from modification.

Proof of Work

Bitcoin makes the addition of a new block – or modification of a block in a blockchain – extremely difficult by creating a puzzle that needs to be solved before the block can be added to the blockchain. By requiring a node to solve a sufficiently difficult puzzle, there will be only a tiny chance that two or more nodes will propose adding a block to the chain simultaneously. It will also make it computationally prohibitive to modify old hash pointers.

This puzzle is called the Proof of Work and is an idea adapted from an earlier system called hashcash. Proof of Work requires computing a hash of three components, hash(B, A, W) where:

• B = block of transactions (which includes the hash pointer to the previous block)
• A = address (i.e., hash of the public key) of the owner of the server doing the computation
• W = the Proof of Work number

When servers are ready to commit a block of transactions onto the chain, they each compute this hash, trying various values of W until the hash result has a specific pre-defined property. The property they are searching for is a hash value that is less than some given number, called the target hash. Currently, it’s a value that requires the leading 17 bits of the 256-bit hash to all be 0s). The property changes over time to ensure that the puzzle never gets too easy or too difficult, regardless of how many nodes are in the network or how fast processors get.

Recall that one property of a cryptographic hash function is the inability to deduce any input by looking at the output. Hence, we have no idea what values of W will yield a hash with the desired properties. Servers have to try trillions of values with the hope that they will get lucky and find a value that yields the desired hash. This process of searching for W is called mining.

When a server finds a value of W that yields the desired hash, it advertises that value to the entire set of bitcoin servers. Upon receiving this message, it is trivial for a server to validate the proof of work by simply computing hash(B, A, W) with the W sent in the message and checking the resultant value. The servers then add the block, which contains the Proof of Work number and the winner’s address, onto the blockchain.

The number of servers and the hardware they use to test hashes changes over time. To account for this, the Bitcoin network’s mining difficulty is periodically adjusted by defining a new target hash. The target hash is periodically recomputed via a Difficulty Adjustment Algorithm (DAA). There have been several versions of this algorithm over time, but they had the same goal. Initially, Bitcoin’s mining difficulty was adjusted every 2,016 blocks, corresponding to approximately 14 days, to keep the average rate at which blocks are added to the blockchain at 10 minutes. Currently, the DAA is more dynamic. It selects a predetermined reference block and compares the timestamps between the reference block and the current block. It then uses that interval to adjust the target hash to predict a value that will keep the hash rate at approximately one block per 10 minutes.

Double Spending and modifying past transactions

A major concern with decentralized cryptocurrency systems is double spending. Double spending refers to sending the same funds (or tokens) to multiple parties: Alice sends $500 to Charles and $500 to David but only has $500 in her account. Bitcoin deals with this by having every server maintain the complete ledger, so Alice’s list of transactions can be validated before a new one is accepted.

Alice may decide to go back to an older transaction and modify it. For example, she might change change the transaction that sent bitcoin to Charles into one that sends money to David – or simply delete the fact that she paid Charles the full amount.

To do this, she would need to compute a new proof of work value for that block so the block hash would be valid. Since Bitcoin uses hash pointers, each block contains a hash pointer to the previous (earlier) block. Alice would thus need to compute new proof of work values for all newer blocks in the chain so that her modified version of the entire blockchain is valid. She ends up building a competing blockchain.

Recomputing the proof of work numbers is a computationally intensive process. Because of the requirement to generate the Proof of Work for each block, a malicious participant will not be able to catch up with the cumulative work of all the other participants. Because of errors or the rare instances where multiple nodes compute the proof of work concurrently, even honest participants may, on occasion, end up building a competing blockchain. Bitcoin’s policy is that the longest chain in the network is the correct one. The length of the chain is the chain’s score and the highest-scoring chain will be considered the correct one by the servers. A participant is obligated to update its chain with a higher-scoring one if it gets notice of a higher-scoring chain from another system. If it doesn’t update and insists on propagating its chain as the official one, its chain will simply be ignored by others.

51% Attack

Let us go back to the example of Alice maliciously modifying a past transaction. In addition to the work of modifying the existing blockchain, Alice will also need to process new transactions that are steadily arriving, and making the blockchain get longer as new blocks get added to it. She needs to change the existing blockchain and also compute proof of work values for new blocks faster than everyone else in the network so that she would have the longest valid chain and hence a high score.

If she can do this then her chain becomes the official version of the blockchain and everyone updates their copy. This is called a 51% attack. To even have a chance of succeeding, Alice would need more computing power than the reset of the systems in the Bitcoin network combined. Back in 2017, The Economist estimated that “bitcoin miners now have 13,000 times more combined number-crunching power than the world’s 500 biggest supercomputers,” so it is not feasible for even a nation-state attacker to harness sufficient power to carry out this attack on a popular cryptocurrency network such as Bitcoin. Blockchain works only because of the assumption that the majority of participants are honest … or at least not conspiring together to modify the same transactions.

Even if someone tried to do this attack, they’d likely only be able to modify transactions in very recent history – in the past few blocks of the blockchain. This is why For this reason, transactions further back in the blockchain are considered to be more secure.

Committing Transactions

Because of the chain structure, it requires more work to modify older transactions (more blocks = more proof of work computations). Modifying only the most recent block is not hugely challenging. Hence, the further back a transaction is in the blockchain, the less likely it is that anyone can amass the computing power to change it and create a competing blockchain.

A transaction is considered confirmed after some number, N, additional blocks are added to the chain. The value of N is up to the party receiving the transaction - a level of comfort. The higher the number, the deeper the transaction is in the blockchain and the harder it is to alter. Bitcoin recommends N=1 for low-value transactions (payments under $1,000; this enables them to be confirmed quickly), N=3 for deposits and mid-value transactions, and N=6 for large payments (e.g., $10k…$1M). Even larger values of N could be used for extremely large payments.

Rewards

Why would servers spend a huge amount of computation, which translates to huge investments in computing power and electricity, just to find a value that produces a hash with a certain property? To provide an incentive, the system rewards the first server (the miner) that advertises a successful Proof of Work number by depositing a certain number of Bitcoins into their account. To avoid rewarding false blockchains as well as to encourage continued mining efforts, the miner is rewarded only after 99 additional blocks have been added to the ledger.

The reward for computing a proof of work has been designed to decrease over time. The reward is halved every 210,000 blocks mined, which is approximately every four years:

• 50 bitcoins for the first 4 years since 2008
• 25 bitcoins after block #210,000 on November 28, 2012
• 12.5 bitcoins after block #420,000 on July 9, 2016 2019
• 6.25 bitcoins at block #630,000 on May 11, 2020
• 3.125 bitcoins at block #840,00 on April 20, 2024

In total, there will be 32 Bitcoin halvings. After that, the reward will reach zero and there will be a maximum of around 21 million bitcoins in circulation. However, recall that each transaction has a fee associated with it. Whoever solves the puzzle first and gets a confirmed block into the blockchain will also reap the sum of all the transaction fees in that block.

Centralization

Bitcoin has been designed to operate as a large-scale, global, fully decentralized network. Anybody can download the software and operate a bitcoin node. All you need is sufficient storage to store the blockchain. There are currently over 15,000 reachable full nodes spread across 84 countries. In this sense, Bitcoin is truly decentralized. Note that there are different types of nodes. The nodes we discussed serve as full nodes. They maintain an entire copy of the blockchain and accept transactions. Light nodes are similar but store only a part of the blockchain, talking to a full node parent if they need to access other blocks.

Not everyone who operates a bitcoin node does mining (proof of work computation). Mining is incredibly time energy intensive. To make money on mining, one needs to buy dedicated ASIC mining hardware that is highly optimized to compute SHA-256 hashes. Conventional computers will cost more in energy than they will earn in bitcoin rewards. Because of this, mining tends to be concentrated among a far smaller number of players. It is not as decentralized as much as one would like.

Bitcoin software is open source but there is only a small set of trusted developers. The software effort is inspectable but not really decentralized. Bugs have been fixed but many nodes still run old and buggy versions. Bitcoin transactions cannot be undone even if they were created by buggy nodes or via compromised keys.

References

• Satoshi Nakamoto, Bitcoin: A Peer-to-Peer Electronic Cash System - the original paper

Info about Bitcoin’s cryptography:

• Andreas M. Antonopoulos, Mastering Bitcoin, 2nd Edition: Chapter 4. Keys, Addresses, O’Reilly Media, June 2007.

• Gayan Samarakoon, ryptographic essence of Bitcoin part # 1: What is a Hash function?, December 28, 2018.

• Gayan Samarakoon, Cryptographic essence of Bitcoin: Part 2 — How do public/private keys work? Elliptical Cryptography & Proof of work, March 22, 2019.

• Raghav Sood, Bitcoin’s Signature Types - SIGHASH

Information about Biutcoin mining difficulty

• Bitcoin difficulty, Bitcoin.it
• Bitcoin target hash, Bitcoin.it
• Difficulty in Mining, Bitcoinwiki.org
• Target: the number you need to get below to mine a block, Learnmeabitcoin.com

Consensus

• Video: High-level intro to the problem: Understanding Consensus Mechanisms, November 21, 2018.

• Video: Understanding Blockchain Consensus mechanisms, March 30, 2019.

• Consensus mechanisms, ethereum.org, January 29, 2022.

Other aspects of Bitcoin:

• Proof of Work Explained in Simple Terms, The Chain Bulletin

• Ameer Rosic, What is Hashing? Step-by-Step Guide Under Hood of Blockchain - tutorial on hashing and hash pointers

• Andreas M. Antonopoulos, Mastering Bitcoin, O’Reilly

  • Chapter 5. Transactions, Mastering Bitcoin, O’Reilly
  • Chapter 8. Mining and Consensus, Mastering Bitcoin, O’Reilly

• Julian Martinez, Part 1: Demystifying Solving a Block, Medium.com, May 2018

• How bitcoin transactions work, Bitcoin.com

Bitcoin statistics:

• Blockcahin Explorer, blockchain.com - real-time visualization
• Total network hashing rate, bitcoin.sipa.be - hash rate graphs

Other info (mostly touching upon Ethereum):

• Intro to Ethereum, February 6. 2022.

• Jim Zhong, What are Smart Contracts and How Do They Work?, Keleido, October 1, 2019

• Consensus Mechanisms, ethereum.org, January 29, 2022.

• [Proof-of-Stake](https://ethereum.org/en/developers/docs/consensus-mechanisms/pos/], ethereum.org, January 26, 2022.

• Proof of Stake FAQs, Ethereum Wiki.